The Theory behind GAN

本文主要介绍了GAN的基础理论。还对似然函数和KL三度的关系进行了推导。

Generation

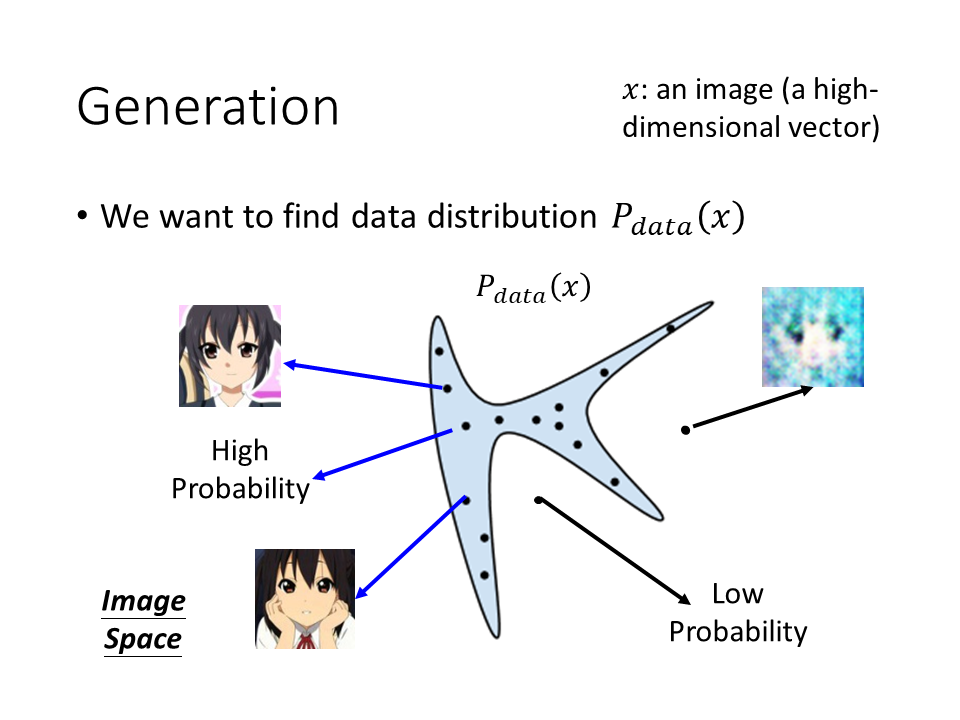
假设我们今天要生成一张image，这里用x来代表一张image，每一张图片都是高维空间中的一个点，图像大小是64 x 64维的，那么vector的维数就是64 x 64，为了方便演示，下图假设图像是二维空间中的一个点。

对于我们要产生的图像，有一个固定的distribution $P$_$data$$(x)$。在整个图像所构成的高维空间中，只有一小部分sample出来的的图像和人脸接近，其他部分都不像人脸。比如我们从下图中蓝色的distribution中进行sample，看起来就很像是人脸（几率是高的），在其他区域就不像人脸（几率是低的）。

那么我们现在的目标就是让机器找到这个distribution。 （但这个distribution长什么样子是不知道的，我们可以收集很多的x得知x可能在某些地方分布比较高。但是把它的式子找出来，我们是不知道怎么做的。）

那么有GAN之前，我们如何做Generate

Maximum Likelihood Estimation

1. 我们可以从这个distribution中sample图像，但我们并不知道对应的formula长什么样子；
2. 那么我们现在可以找到另外一个distribution $P_G(x,\theta)$,比如其对应参数可以是$\mu,\sum$,来使这个distribution的参数和原来的接近

具体做法如下，

• 先从原来的distribution中sample出${x^1,x^2,…,x^m}$;
• 把$x^i$代入现在的已知的distribution$P_G(x^i,\theta)$,表示$x^i$是从现在这个distribution中sample出来的概率
• 把这些概率相乘，得到似然函数L；最后找到对应的参数$\theta$,使似然函数取得最大值

Minimize KL Divergence

最大似然估计也就等同于来最小化KL divergence(KL 散度)。

Tip：大数定理：独立同分布时，抽样均值等于总体期望

最小交叉熵是采样数据分布和生成分布的差距最小。

(不加是对数似然函数，加上负号是交叉熵，最小化交叉熵等价于最大似然，加上是KL散度。)

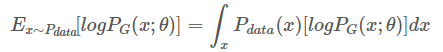
现在我们的问题是找到参数$\theta^*$,使得E_x~Pdata[$logP_G(x;\theta)$]可以取最大值。${x^1,x^2,…,x^m}$是从distribution $P$_$data$中sample出来的，我们把这里的$E$_x~Pdata展开，从离散值变到连续值，即：

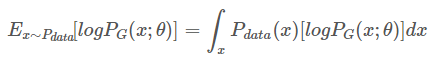
由于我们的目标是找到$P_G$分布对应的参数，现在加入一个常数项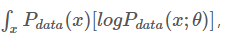，对最大化问题也不会产生影响，即：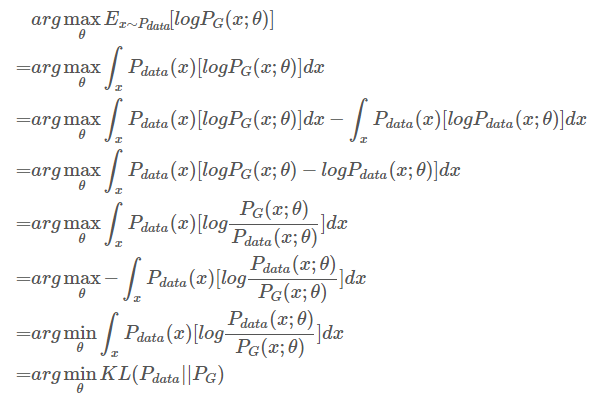

就把这个最大化似然函数问题转化为了最小化KL divergence的问题。

那么我们如何来定义$P_G$的表达式呢？

首先$P_G$是类似于高斯分布这样的distribution，很容易计算出其对应的likelihood；但如果是neural network这样的distribution，就很难算出这个likelihood。